Ca. 90 % van de toepassingen kan aan de hand van de volgende vijf gegevens makkelijk worden berekend:
- Af te remmen massa (gewicht) m [kg]
- Stoot- of botssnelheid vD [m/s]
- Evt. aanwezige aandrijfkracht F [N]
- Aantal slagen of cycli per uur x [1/h]
- Aantal stootdempers parallel n
Gebruikte formuletekens
| Afkorting | Unit | Beschrijving | Afkorting | Unit | Beschrijving |
|---|---|---|---|---|---|
| W1 | Nm | kinetische energie per slag; a.g.v. de massa | 3ST | 1 tot 3 | aanloopkoppel factor (normaal 2,5) |
| W2 | Nm | energie van de aandrijfkracht per slag | M | Nm | aandrijfkoppel |
| W3 | Nm | totale energie per slag (W1 + W2) | I | kgm2 | massatraagheidsmoment |
| 1W4 | Nm/hr | totale energie per uur (W3 · x) | g | m/s2 | valversnelling = 9,81 |
| me | kg | effectieve massa | h | m | valhoogte zonder stootdemperslag |
| m | kg | af te remmen massa | s | m | slaglengte stootdemper |
| n | aantal stootdempers (parallel) | L/R/r | m | straal | |
| 2v | m/s | snelheid bij de botsing | Q | N | reactiekracht |
| 2vD | m/s | botssnelheid opde stootdemper | μ | wrijvingscoëfficient | |
| ω | rad/s | hoeksnelheid bij de botsing | t | s | afremtijd |
| F | N | aandrijfkracht | a | m/s2 | vertraging |
| c | 1/hr | aantal slagen per uur | α | ° | botshoek |
| P | kW | motorvermogen | β | ° | hoek |
Voor alle voorbeelden geldt:
Bij gebruik van meerdere dempers parallel worden de waarden W3, W4 en me door het aantal dempers gedeeld.
|
Reactiekracht Q [N] Q = (1,5 · W3) / s |
Afremtijd t [s] t = (2,6 · s) / vD |
Vertraging a [m/s2] a = (0,75 · vD2) / s |
De formules voor de berekening van de reactiekracht, afremtijd en vertraging hebben alleen betrekking op industriestootdempers van ACE. Bij instelbare ACE industriestootdempers gelden deze3 formules alleen bij de juiste instelling. Hanteer een veiligheidsmarge. Bij veiligheidsstootdempers gelden andere formules. Neem hiervoor contact op met ACE.
Toepassingen
| Toepassing | Formule | Voorbeeld | |
|---|---|---|---|
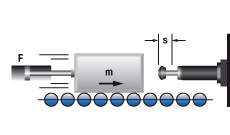
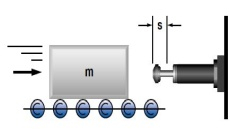
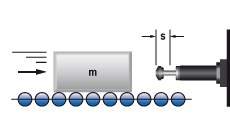
1. Massa zonder aandrijfkracht
|
W1 = m · v2 · 0,5
W2 = 0
W3 = W1 + W2
W4 = W3 · x
vD = v
me = m
|
m = 100 kg W1 = 100 · 1,52 · 0,5 = 113 Nm |
|
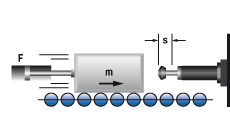
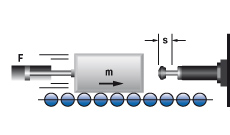
2. Massa met aandrijfkracht
|
W1 = m · v2 · 0,5
W2 = F · s
W3 = W1 + W2
W4 = W3 · x
vD = v
me = (2 · W3) / vD2
2.1 Bij verticale beweging omhoog
W2 = (F – m · g) · s
2.2 Bij verticale beweging omlaag
W2 = (F + m · g) · s
|
m = 36 kg
1v = 1,5 m/s
F = 400 N
x = 1000 1/h
s = 0,025 m (gewählt)
W1 = 36 · 1,52 · 0,5 = 41 Nm
W2 = 400 · 0,025 = 10 Nm
W3 = 41 + 10 = 51 Nm
W4 = 51 · 1000 = 51000 Nm/h
me = 2 · 51 : 1,52 = 45 kg
1 v is the fi nal impact velocity of the mass:
With pneumaticallypropelled systems this can be 1.5 to 2 times the average velocity. Please take this into account when calculating energy. |
|
3. Massa met aandrijfkracht (geometrisch)
|
W1 = m · v2 · 0,5
W2 = (1000 · P ·HM · s) / v
W3 = W1 + W2
W4 = W3 · x
vD = v
me = (2 · W3) / vD2
|
m = 800 kg W1 = 800 · 1,22 · 0,5 = 576 Nm motor, coupling and gearbox into calculation for W1 |
|
4. Massa op aangedreven rollen (met frictie)
|
W1 = m · v2 · 0,5
W2 = m · μ · g · s
W3 = W1 + W2
W4 = W3 · x
vD = v
me = (2 · W3) / vD2
|
m = 250 kg W1 = 250 · 1,52 · 0,5 = 281 Nm |
|
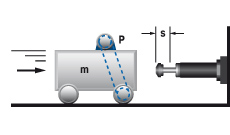
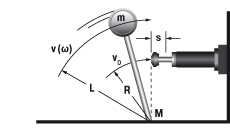
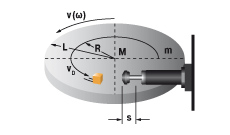
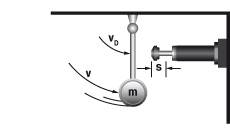
5. Zwenkende massa met aandrijfkracht
|
W1 = m · v2 · 0,5 = 0,5 · J · ω2
W2 = (M · s) / R
W3 = W1 + W2
W4 = W3 · x
vD = (v · R) / L = ω · R
me = (2 · W3) / vD2
|
m = 20 kg W1 = 20 · 12 · 0,5 = 10 Nm |
|
6. Massa in vrij e val
|
W1 = m · g · h
W2 = m · g · s
W3 = W1 + W2
W4 = W3 · x
vD = √2 · g · h
me = (2 · W3) / vD2
|
m = 30 kg W1 = 30 · 0,5 · 9,81 = 147 Nm |
|
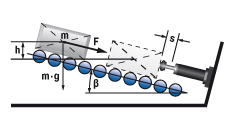
6.1 Massa op hellend vlak
|
W1 = m · g · h = m · vD2 · 0,5
W2 = m · g · sinβ · s
W3 = W1 + W2
W4 = W3 · x
vD = √2 · g · h
me = (2 · W3) / vD2
6.1a Bij verticale beweging omhoog
W2 = (F – m · g· sinβ) · s
6.1b Bij verticale beweging omlaag
W2 = (F + m · g· sinβ) · s
|
m = 500 kg W1 = 500 · 9,81 · 0,1 = 490,5 Nm |
|
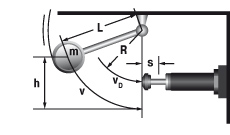
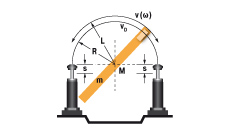
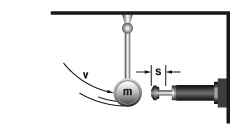
6.2 Massa vrij zwenkend
|
W1 = m · g · h
W2 = 0
W3 = W1 + W2
W4 = W3 · x
vD = √2 · g · h · (R / L)
me = (2 · W3) / vD2
tan α = s / R
|
m = 50 kg W1 = 50 · 9,81 · 1 = 490,5 Nm |
|
7. Draaitafel met aandrij fkoppel horizontaal of verticaal
|
W1 = m · v2 · 0,25 = 0,5 · J · ω2
W2 = (M · s) / R
W3 = W1 + W2
W4 = W3 · x
vD = (v · R) / L = ω · R
me = (2 · W3) / vD2
|
m = 1000 kg W1 = 1000 · 1,12 · 0,25 = 303 Nm |
|
8. Zwenkende massa met aandrijf-koppel (bij v. keer-inrichting)
|
W1 = m · v2 · 0,17 = 0,5 · J · ω2
W2 = (M · s) / R
W3 = W1 + W2
W4 = W3 · x
vD = (v · R) / L = ω · R
me = (2 · W3) / vD2
|
J = 56 kgm2 W1 = 0,5 · 56 · 12 = 28 Nm |
|
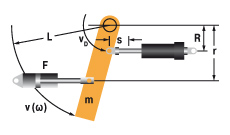
9. Zwenkende massa met aandrijfkracht
|
W1 = m · v2 · 0,17 = 0,5 · J · ω2
W2 = (F · r · s) / R = (M · s) / R
W3 = W1 + W2
W4 = W3 · x
vD = (v · R) / L = ω · R
me = (2 · W3) / vD2
|
m = 1000 kg W1 = 1000 · 22 · 0,17 = 680 Nm |
|
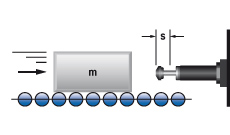
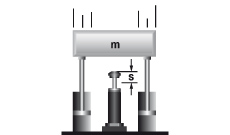
10. Massa zonder aandrijfkracht
|
W1 =m · v2 · 0,5
W2 = m · g · s
W3 = W1 + W2
W4 = W3 · x
vD = v
me = (2 · W3) / vD2
|
m = 6000 kg W1 = 6000 · 1,52 · 0,5 = 6750 Nm |
|
Effectieve massa (me)
De effectieve massa (me) is de werkelijke massa in beweging (voorbeeld A en C), deze massa
vermeerderd met een theoretische massa uit aandrijfkracht of overbrenging (voorbeeld B en D).
| Toepassing | Voorbeeld |
|---|---|
A Massa zonder aandrijfkracht
|
m = 100 kg
vD = v = 2 m/s
W1 = W3 = 200 Nm
me = (2 · 200) / 4 = 100 kg
FORMULA: ME = M
|
B Massa met aandrijfkracht
|
m = 100 kg
F = 2000 N
vD = v = 2 m/s
s = 0,1 m
W1 = 200 Nm
W2 = 200 Nm
W3 = 400 Nm
me = (2 · 400) / 4 = 200 kg
FORMEL: ME = (2 · W3) / VD2
|
C Massa zonder aandrijfkracht direct op de stootdemper
|
m = 20 kg
vD = v = 2 m/s
W1 = W3 = 40 Nm
me = (2 · 40) / 22 = 20 kg
FORMEL: ME = M
|
D Massa zonder aandrijfkracht met hefboomoverbrenging
|
m = 20 kg
v = 2 m/s
vD = 0,5 m/s
s = 0,1 m
W1 = W3 = 40 Nm
me = (2 · 40) / 0,52 = 320 kg
FORMEL: ME = (2 · W3) / VD2
|